むずいよ〜、、、、、

１）フェルミ分布　（Fermi distribution function）

　　電子が、エネルギー別にどんなけ　いるか？（占有率）です。

　　フェルミ・ディラック分布関数（Fermi-Dirac distributin function）、、ちゅうややこしい式で計算されます。

　　フェルミ粒子（Fermion）（例：電子）は、この式に従うそうです。。。　　→フェルミ粒子って、、　パウリの排他原理に従う粒子、、らしい。

　　で、フェルミ、フェルミといってますが、”フェルミ”ちゅうのは、イタリアの物理学者（エンリコ・フェルミ）のおっさんの名前。　

　　で、　イメージちゅうやつは、、、うーん、、、、　箱の中にビー玉つめて、がちゃがちゃ振った時に、

　　早く動いているやる、遅いやつがどれだけいるかって感じかな？？？

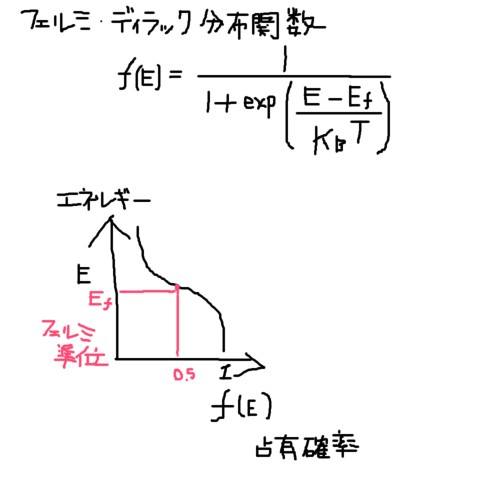
　　フェルミ準位（Ｅｆ）とは、電子の占有率が５０％のとこのエネルギーです。

　　ただ、、、よーわからんのが、これは、半導体のようにとびとびの電子状態に適用していいのか？？？

　　金属ならよさそうな気がするんだが、、、　不思議。。。　

２）状態密度　（density of states）

　　電子が入れる箱です。

　　詳しくは、なにやら難しいことをこちょこちょするとでてきます。

　　Ｅｃ：　伝導帯の底のエネルギーレベル

　　Ｅｖ：　価電帯の頂上のエネルギーレベル

３）キャリア密度

　　フェルミ分布　ｘ　状態密度　です。

　　キャリア（＝電子）が結局、このくらいいるよーってことです。

　　で、計算は、、、ここからがややこしい。。。　とりあえず、途中まで。

　　１）まずは、フェルミ分布を、ボルツマン分布ちゅうのに近似します。

　　　　なぜ近似するかって？？？　計算が簡単になるし、半導体の実際に使うあたりでは、

　　　　まあこんなもんでＯＫなので、、、。

　　　　Ｓｉ（シリコン）の禁制帯幅（Ｅｇ）は、Ｅｇ＝１．１２[ｅＶ]。

　　　　対して、ＫｂＴは、

　　　　Ｋｂ＝ボルツマン定数＝１．３８０６５０３　ｘ　１０−２３　[ｍ２ｋｇｓ−２Ｋ−１]

　　　　Ｔ＝温度＝適当。。。

　　　　だと、Ｅｇ＞＞ＫｂＴ　だす。　”＞＞”は、すっごーーーーく差があるちゅうことです。

　　　　でだ。　Ｅ−Ｅｆ　も、だいたーい。　ＫｂＴよりすっごーく大きい。　かな〜。。。

　　　　そうすっと、ｅｘｐ（Ｅ−Ｅｆ）／ＫｂＴ＞＞１。

　　　　、、、にゃー。　ここから先は、また今度。

おわり。